Bewijsconstructie

Hoe komt een bewijs tot stand?

1. Intuitie (incl. inductie), inspiratie en geluk.
2. Ervaring
3. Het eerder gezien hebben van een soortgelijk theorema en het bewijs daarvan.
4. Begrip van het te bewijzen theorema
5. Voorbeelden maken (draagt bij aan begrip)
6. Eerst een speciaal geval bewijzen
7. De conclusie niet vergeten - waar men naartoe moet werken
8. Van en naar de conclusie af en toe werken - vooral als het theorema in een als-dan theorema is door de transitiviteit van =>
9. Is lineair bezig zijn de beste manier? Een bewijs kan ook in stukken gebroken worden - top-down approach. Leron (1983) schrijft dat (complexe) bewijzen zo beter begrijpelijk zijn en dus in ieder geval beter zo gepresenteerd kunnen worden.

Inhoud

1 Rechtvaardiging transitiviteit 2 Top-down approach 1 Voorbeelden 1.1 Even kwadraat 1.2 Verzamelingen 1.3 Perpetuum mobile

Rechtvaardiging transitiviteit

Als P=>Q en Q=>R, dan zijn P->Q en Q->R theorema van het onderliggende axiomatische systeem. Maar dan is ->R ook een theorema van het onderliggende axiomatische systeem - dat kan gezien worden door gebruik te maken van HS. Dus P=>R.

Opmerking: '=>' is ook een reflexieve relatie (dus P=>P), maar geen symmetrische relatie (dus niet noodzakelijkerwijs als P=>R, dan R=>P). In die gevallen waar dit wel zo is, gebruiken we P<=>R.

Top-down approach

In de top-down approach van bewijzen zijn er drie niveaus te onderscheiden. Het hoogste niveau is de algemene structuur van een bewijs - wat hebben we nodig. Een niveau lager: van premissen naar conclusie werken zonder zich te bekommeren over details of dingen die we niet meteen kunnen bewijzen en hier gewoon aannemen. Nog een niveau lager komen de specifieke bewijzen - de lemma's, ...

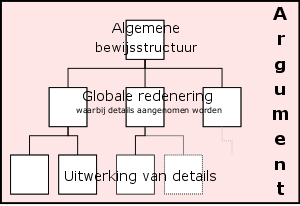
Voorbeelden

Even kwadraat

Het kwadraat van om het even welk even getal is even.
Of: Alle even getallen hebben even kwadraten ∀x[E(x)→E(x²)], en met UC: E(n)→E(n²).
Of: Een even getal heeft een even kwadraat. E(n)→E(n²).

Definitie: n is een even geheel getal iff er een geheel getal m bestaat zodanig dat n=2m.

Bewijs:

• Laat n een even geheel getal zijn
• Dan n=2m voor een geheel getal m
• Dan n² = (2m)² = 2(2m²) = 2M, waar M=2m² een geheel getal
• Dus n² is even. Δ

En wat formeler:

• n is een even geheel getal
• => n=2m, m geheel getal
• => n²=(2m)²=4m²=2(2m²)
• => n²2M, M=2m²
• => n² even. Δ

Verzamelingen

Voor elke twee arbitraire verzamelingen A en B geldt dat (A\B)∩B = ∅

Bewijs:

• Neem aan dat er een element a bestaat zodat a∈(A\B)∩B zodanig dat
• => a∈A∩B & a∈B
• => a∈A & a∈B & a∈B
• 

(hierin is B het complement van B, alles wat niet in verzameling B zit.)

Dus er bestaat niet een element a zodat a∈(A\B)∩B dus (A\B)∩B=∅

Perpetuum mobile

Achtergrondkennis: klassieke natuurkunde

Een perpetuum mobile is letterlijk een ding dat beweegt. Er wordt mee bedoeld: een machine die arbeid kan verrichten zonder dat je energie toevoegt. Dat een perpetuum mobile niet bestaat is een axioma in de natuurkunde. Het is nooit aangetoond dat het niet kan bestaan, maar het is nog nooit gevonden. Het axioma wordt uitgedrukt in de wet van behoud van energie.

De wet van behoud van energie voor een geïsoleerd systeem is: "energie kun je wel omzetten van de ene soort in de andere, maar je kunt energie niet maken of vernietigen". Hierin is een geïsoleerd systeem een ruimte waar geen energie in of uit kan.

Nu een toepassing van dit axioma. Dat veldlijnen loodrecht op geleiders staan, is een natuurkundige wet. Een informeel bewijs uit het ongerijmde volgt.

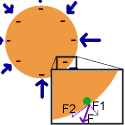
We hebben een cylinder met een negatieve lading. Stel nu dat er een veldlijn is die niet loodrecht op de cylinder staat. Dan ondervindt een electron e een kracht F met de componenten F1 loodrecht op de geleider en F2 evenwijdig met de raaklijn aan de geleider. Omdat de veldlijn niet loodrecht op de geleider staat, zal het electron een kracht naar F2 beneden ervaren. Hierdoor gaat het electron bewegen evenwijdig met de rand van de cylinder. Even later is 'ie weer terug op de eerste plaats, en daar krijgt het weer een zetje naar beneden. Het electron gaat steeds sneller, de temperatuur stijgt en de cylinder smelt.

Dit is in strijd met het axioma van het perpetuum mobile, hierdoor is er een tegenspraak. De aanname dat er een veldlijn is die niet loodrecht op de cylinder staat is onjuist, dus alle veldlijnen staan loodrecht op de geleider.